本文主要内容来自 Data Structures Course Lecture Notes ; Log Structured Merge Trees; Algorithms Behind Modern Storage Systems Different uses for read-optimized B-trees and write-optimized LSM-trees;

binary tree(二叉树)

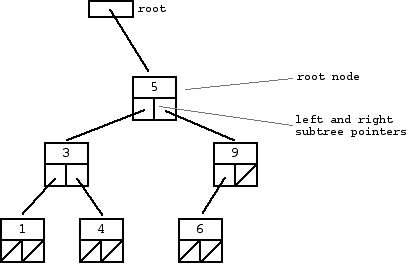二叉树有一个根节点（root node）,其左边（left child）同样是一个子二叉树（subtrees），右边(right child)也是一个子二叉树。左边或右边可以是空，或者两边都是空。

binary search tree BST（查找二叉树，有序二叉树）

每个节点N的左边子节点都小于或等于(<=)节点N,每个节点N的右边子节点都大于(>)节点N. 在查找二叉树中没有任何子节点的节点称为叶子节点(leaf node),相对的，其他节点则为内部节点(internal node).

Degenerate tree, or linear tree（退化树,线性树）

情况最不利于查找的树

Height of the tree(树的高度)

一个节点的高度指的是其最远叶子节点到这个节点的路径经过的边。 那么一个树的高度指的是根结点的高度。 附带说一下，一般Depth指的是节点到根节点的路径经过的边，但有时说depth就是指的height。

Balanced Trees(平衡二叉树)

perfectly height-balanced tree (完美平衡二叉树)

每个节点的左子树和右子树的高度保持一致则是完美平衡二叉树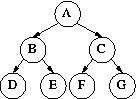

height-balanced tree(平衡二叉树)

每个节点的左右子节点的height差不超过1的称为平衡二叉树，其包括了完美二叉树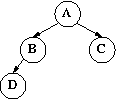

AVL trees，Height-Balanced Binary Search Trees（AVL树，平衡二叉搜索树）

AVL命名来自其俄国发明者Adelson-Velskii and Landis。 平衡二叉树的特性加上搜索树的特性就是AVL树。 可以证明Height < 1.5logN,AVL树的 AVL树可以保证搜索，插入，删除的效率为 O(logN)

旋转（rotation）-不平衡(imbalance)到再平衡(re-balance)

一个完美AVL树 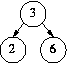insert 1 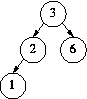insert 0 – imbalance 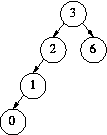rotation 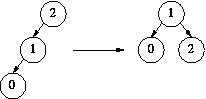re-balance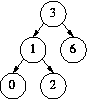

B-Tree

B-Tree名字来自发明者Boyer,其当时工作于波音.

M-way Search Trees

M-way Search Trees就是子树大于2个的二叉搜索树，M表示子节点分支个数，例如，二叉树的M就是2. 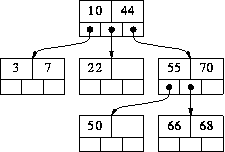其特点是对于实际应用来说，其M相当大，常常对应硬盘中的每一个块(block)一个页(page)甚至跨页。

B-trees: Perfectly Height-balanced M-way search trees

B-Trees就是一个M-way Search Trees，又有其新特点： 1：它是完美平衡树 2：除了根节点，所有节点的值个数>M/2且<=M-1,根节点值个数为>=1且<=M-1个。
例子：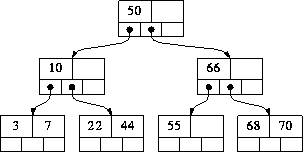

B-trees插入值的例子

1：插入前 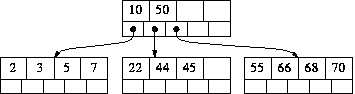2：插入17后 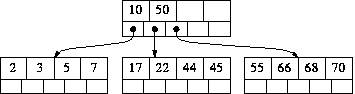3：再插入5 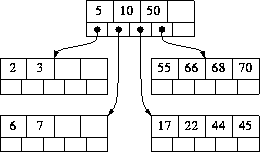从中可以看出，与二叉搜索树不同的是，每次增加节点可能导致的是父节点的值的增加或分裂，不会导致不平衡而需要再平衡。

由此不难看出Binary Trees和B-Trees的区别，就像数组和链表的关系，数组增删一个元素会导致整个数组重构，而链表则只需要修改某个节点的指针。数组更适合内存中存储较小的内容，链表适合应用在硬盘中实现存储较大的内容。 ####

LSM-Trees (Log Structured Merge Trees)

LSM-Trees由google发表于1996，其原来用于big-table. 主要关注的是写操作的性能，原理基于一个基础的认知： 对硬盘的写操作，顺序写要比随即写快很多倍，差不多达到200-300MB每秒。 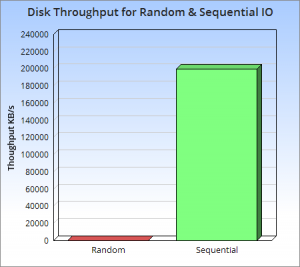这种方式，通常被称为logging, journaling 或 heap file。 不过任何事都有两面，类似磁带机，写可以很快的顺序写，要读某个点的数据，那就有点慢了。

LSM-Trees的基本理念

对于数据库写，需要创建索引，还要依据新数据更新索引，如果使用一个大文件记录所有索引，则会很慢（查找，插入，删除）。因此LSM-Trees做法就是：

• 使用小文件，每个写的时间段对应一个索引。在写之前排序，由于小，所以快。
• 写后文件就不会更改，如果需要更新，则在新的文件中写。
• 读会检查所有的文件，然后隔时间段整合（merge），从而控制总的文件大小。

更多细节

一般LSM-Trees会配合内存排序，内存里将写数据缓冲（通常是一个(Red-Black Tree)红黑树结构），在写之前排序，然后再写入硬盘–总之，要确保写硬盘操作是序列化的。

对于读，由于文件是排序的，这也提高了读的效率，一般都会将文件索引到内存中或者直接将索引写在每个文件的末尾。

Red-Black Tree(红黑树)

红黑树也是一种BST(二叉搜索树)

其有以下特点：

• 根节点是黑色
• 红色节点的子节点必须是黑色，黑色节点的子节点可以是红或者黑
• (For each node with at least one null child, the number of black nodes on the path from the root to the null child is the same.)结点到其子孙结点的每条简单路径都包含相同数目的“黑色”结点
• 它不要求是平衡树
• 复杂度依然是O(logN)(注意网上说O(log2n)什么的，和O(logN)是一个意思，简单说O(Big O)对底数不敏感)

从根结点到叶结点的黑色结点数被称为树的“黑色高度”(black-height)。前面关于红黑树的性质保证了从根结点到叶结点的路径长度不会超过任何其他路径的两倍。

我们来解释一下这个结论。考虑一棵黑色高度为3的红黑树：从根结点到叶结点的最短路径长度显然是2(黑-黑-黑)，最长路径为4(黑-红-黑-红- 黑)。由于性质4，不可能在最长路经中加入更多的黑色结点，此外根据性质3，红色结点的子结点必须是黑色的，因此在同一简单路径中不允许有两个连续的红色结点。综上，我们能够建立的最长路经将是一个红黑交替的路径。

由此我们可以得出结论：对于给定的黑色高度为n的红黑树，从根到叶结点的简单路径的最短长度为n-1，最大长度为2(n-1)。

红黑树能够以O(logN)的时间复杂度进行搜索、插入、删除操作。此外，由于它的设计，任何不平衡都会在三次旋转之内解决。当然，还有一些更好的，但实现起来更复杂的数据结构能够做到一步旋转之内达到平衡，但红黑树能够给我们一个比较“便宜”的解决方案。红黑树的算法时间复杂度和AVL相同，但统计性能比AVL树更高。

AVL树和红黑树的性能，各有各的说法，并不能绝对的说那个算法更快。一般认为红黑树牺牲平衡性达到较快的插入，删除性能。 但其旋转（rotation)的实现，调试较复杂。 使用红黑树的例子:

• Java: java.util.TreeMap , java.util.TreeSet .
• C++ STL: map, multimap, multiset.
• Linux kernel: completely fair scheduler, linux/rbtree.h

总结

简单来说B-Trees读起来快，LSM-Trees写起来快，读写都快的算法还没出来，所以目前大部分数据库都是混合使用这两种算法。

Refs:

红黑树的优点